| CPC H04L 9/008 (2013.01) [G06F 17/16 (2013.01)] | 5 Claims |
|
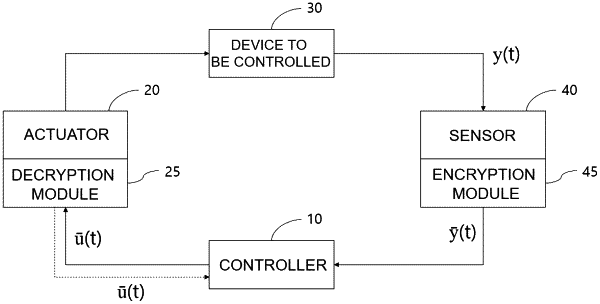
1. A computer-implemented method for processing dynamic data in the environment comprising a device to be controlled, a controller generating a control command (u(t)), a decryption module which decrypting an encrypted control command received from the controller, an actuator which operates according to the decrypted control command received from the decryption module, a sensor which detects the output (y(t)) of the device and an encryption module which homomorphically encrypts the signal of the sensor, the method comprising:
transforming, by the controller, an original state-space representation of the controller “x(t+1)=Fx(t)+Gy(t),u(t)=H x(t)+Jy(t)” into
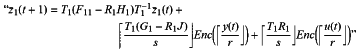 (z1T1w11/s (scaling factor) is larger than 1; r (resolution) is larger than zero; w1 is a variable of the state-space representation of the controller after Kalman observable decomposition is carried out to the original state-space representation of the controller); and
calculating, by the controller, R1 and T1 which makes T1(F11−R1H1)T1−1 an integer matrix;
wherein calculating R1 and T1 comprises calculating the eigenvalues of F11 as λ1, . . . , λm1, σ1±iω1, . . . , σm2±iωm2; calculating R1 through pole placement method, R1 making the eigenvalues of “F11−R1H1” equal to ┌λ1┘, . . . , ┌λm1┘, ┌σ1┘±i┌ω1┘, . . . , ┌σm2┘±┌ωm2┘; calculating T1 which transforms F11−R1H1 into a modal canonical form; and reflecting the calculated integer matrix T1(F11−R1H1)T1−1 as the state matrix of the transformed state-space representation of the controller; and
wherein F11 and H1 are obtained from w1(t+1)=F11w1(t)+G1y(t) and u(t)=H1w1(t)+Jy(t) which are transformed state-space representation of the of the controller, the transformed state-space representation being obtained by carrying out Kalman observable decomposition to the original state-space representation, wherein T1, F11, R1, and H1 are transformation matrices.
|