| CPC G06F 17/16 (2013.01) | 20 Claims |
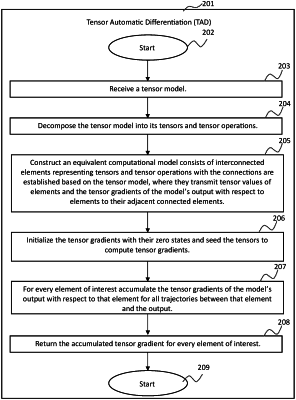
|
1. A method for efficient and automatic computation of tensor gradients of a user-defined computational model, whose inputs includes a tensor product, which is an output of a tensor contraction of at least two contracting tensors, with respect to said contracting tensors, in a computer-based environment, given the tensor product's gradient, which is the gradient of said computational model's output with respect to the tensor product, comprising:
receiving the contracting tensors, a list of contracting dimensions, and the tensor product's gradient;
verifying that the contracting tensors have equal dimension sizes along their contracting dimensions;
applying a search algorithm to determine a transformation for each of the contracting tensors such that said transformations when applied on said contracting tensors do not alter an equivalent tensor contraction's product;
computing transformed tensors by transforming said contracting tensors using said transformations;
computing auxiliary tensor gradients by a tensor contraction, which is defined based on said equivalent tensor contraction's differentiation, between the transformed tensors and the tensor product's gradient; and
computing tensor gradients of said computational model with respect to said contracting tensors by applying inverse functions on said auxiliary tensor gradients reversing the applied transformations;
wherein tensor contraction defined on at least two contracting tensors refers to a tensor operation that performs tensor inner product, also known as tensor dot product, over no, one, or several contracting dimensions of the contracting tensors, while implicitly resulting an outer product along the rest of the dimensions, and consequently, if there are no contracting dimensions, it results in a tensor outer product of the contracting tensors; and wherein the tensors and tensor gradients are represented in a computer-based format; and wherein all tensors, tensor gradients and operations are subject to the numerical precision of the same machine on which said computational model is defined and on which said tensor gradients are automatically computed.
|