US 12,122,359 B2
Coordinated control method for electric vehicles having independent four-wheel driving and steering
Hong Chen, Shanghai (CN); Lin Zhang, Shanghai (CN); Rongjie Yu, Shanghai (CN); and Hanghang Liu, Shanghai (CN)
Assigned to tongji University
Filed by Tongji University, Shanghai (CN)
Filed on Oct. 18, 2023, as Appl. No. 18/381,352.
Prior Publication US 2024/0270235 A1, Aug. 15, 2024
Int. Cl. B60W 30/02 (2012.01); B60L 15/20 (2006.01); B60W 10/08 (2006.01); B60W 10/119 (2012.01); B60W 10/20 (2006.01); B60W 40/114 (2012.01)
CPC B60W 30/02 (2013.01) [B60L 15/20 (2013.01); B60W 10/08 (2013.01); B60W 10/119 (2013.01); B60W 10/20 (2013.01); B60W 40/114 (2013.01); B60L 2240/463 (2013.01); B60W 2510/222 (2013.01); B60W 2520/10 (2013.01); B60W 2520/14 (2013.01); B60W 2520/20 (2013.01); B60W 2520/30 (2013.01); B60W 2710/207 (2013.01); B60W 2720/30 (2013.01)] 10 Claims
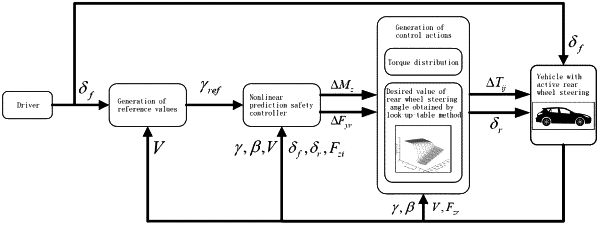
OG exemplary drawing
 
1. A method for coordinated control of an electric vehicle having independent four-wheel driving and steering, the method comprising:
performing a steering angle control based on a current vehicle motion state;
calculating a desired value of yaw velocity in a reference value generation module based on the steering angle control and a current vehicle driving speed,
constructing an optimization problem in a prediction controller based on the current vehicle motion state and calculating the desired value of yaw velocity by the reference value generation module, wherein an objective function of the optimization problem includes tracking the yaw velocity,
inhibiting a mass center side slip angle, adjusting an active rear wheel steering angle and an additional yaw moment control variable in a coordinated manner;
solving the optimization problem to obtain a desired active rear wheel steering angle control variable and a desired additional yaw moment control variable;
calculating an additional torque of each wheel in the control action generation module according to the desired additional yaw moment control variable;
obtaining the desired active rear wheel steering angle using a look-up table method based on a desired lateral force; and
transmitting the calculated additional torque of each wheel and the desired active rear wheel steering angle to an executor of the vehicle performing a coordinated control based on the additional torque of each wheel and the desired active rear wheel steering angle;
wherein
the fast solving of the original optimization problem, comprising the steps of:
converting a to-be-optimized problem into an explicit solving problem based on the Pontryagin extremum principle,
finding an initial value of an optimal co-state variable by means of particle swarm optimization, and
indirectly solving the original optimization problem based on the initial value of the optimal co-state variable.