| CPC B60L 53/37 (2019.02) [B25J 9/163 (2013.01); B25J 9/1687 (2013.01); B25J 9/1697 (2013.01); B25J 13/08 (2013.01); B60L 53/16 (2019.02); G06N 3/08 (2013.01); G06T 7/73 (2017.01); G05B 2219/40269 (2013.01); G06T 2207/10024 (2013.01); G06T 2207/10028 (2013.01); G06T 2207/20081 (2013.01); G06T 2207/20084 (2013.01)] | 19 Claims |
|
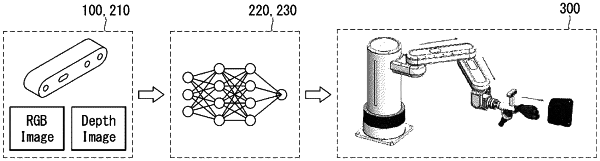
1. A method of controlling an autonomous electric vehicle charging robot, the method comprising:
acquiring, by an image sensor, an RGB image and a depth map of a charging socket of an electric vehicle;
detecting, by a processor, keypoints of the charging socket based on the RGB image;
deriving, by the processor, a first estimated pose of the charging socket based on the depth map;
deriving, by the processor, a second estimated pose of the charging socket based on the keypoints of the charging socket and the first estimated pose; and
driving a charging connector of the autonomous electric vehicle charging robot according to the second estimated posture of the charging socket so that the charging connector is moved to be aligned with the charging socket and is inserted into the charging socket,
wherein the deriving the first estimated pose of the charging socket comprises:
correcting the depth map of the charging socket by interpolating the depth map;
deriving an equation of a plane of the charging socket by sampling a plurality of internal points inside a corrected depth map;
projecting the keypoints of the charging socket onto the plane represented by the equation to acquire projection coordinates;
acquiring reference coordinates (qi) corresponding to the projection coordinates (pi) from a CAD model of the charging socket; and
acquiring an initial transformation matrix describing the first estimated pose and minimizing differences between the projection coordinates (pi) and the reference coordinates (qi), wherein the deriving the second estimated pose of the charging socket comprises:
deriving an optimal transformation matrix describing the second estimated pose, comprising an optimal rotation matrix and an optimal translation vector, and minimizing differences between coordinates of the keypoints (yi) and the reference coordinates (qi) corresponding to the keypoints.
|