| CPC G06Q 10/06 (2013.01) [G06Q 10/0631 (2013.01); G06Q 10/0637 (2013.01); G06Q 10/06375 (2013.01); G06Q 10/087 (2013.01)] | 17 Claims |
|
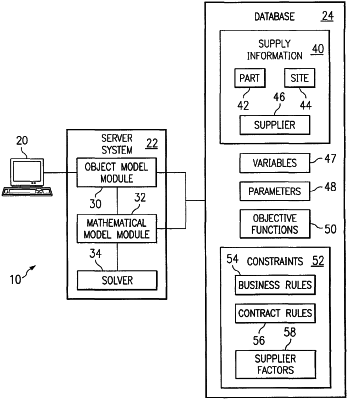
1. A system of supply allocation, comprising:
a system architecture having a mathematical model module, a solver, an object model module, a database and a computer, comprising a processor and memory, wherein the mathematical model module, the solver and the object model module further comprise JAVA BEAN components residing in a container, the computer configured to:
generate, using the mathematical model module based on data retrieved from the database, a mathematical model that represents objectives of an allocation plan by at least two objective functions, a supply quantity by a part variable, and a supply cost by a cost function;
solve, using the solver, the mathematical model for the at least two objective functions and restricted by one or more first constraints by:
weighting one or more values of a first objective function of the at least two objective functions;
weighting one or more values of a second objective function of the at least two objective functions; and
solving a combined objective function comprising weighted first and second objective functions; and
calculate, using the object model module, a quantity of parts to procure from at least one supplier based on the part variable of the solved mathematical model.
|