	US 12,112,110 B2
	Multi-physics co-simulation method of power semiconductor modules
Zhiqiang Wang, Wuhan (CN); Yayong Yang, Wuhan (CN); Yuxin Ge, Wuhan (CN); Guoqing Xin, Wuhan (CN); and Xiaojie Shi, Shenzhen (CN)
Assigned to Huazhong University of Science and Technology, Wuhan (CN); and Shenzhen Union Semiconductor Co., LTD, Shenzhen (CN)
Filed by Huazhong University of Science and Technology, Wuhan (CN); and Shenzhen Union Semiconductor Co., LTD, Shenzhen (CN)
Filed on Aug. 18, 2022, as Appl. No. 17/890,354.
Claims priority of application No. 202110963062.2 (CN), filed on Aug. 20, 2021.
Prior Publication US 2023/0057941 A1, Feb. 23, 2023
Int. Cl. G06F 30/367 (2020.01); G06F 30/31 (2020.01); G06F 30/398 (2020.01)

CPC G06F 30/367 (2020.01) [G06F 30/31 (2020.01); G06F 30/398 (2020.01)]

3 Claims

1. A multi-physics co-simulation method of a power semiconductor module, comprising the following steps:

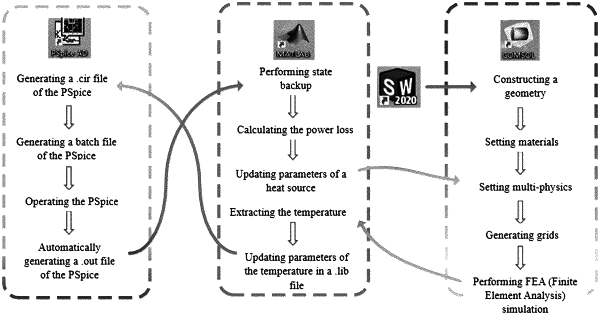
step 1, predefining parameters, performing a circuit simulation under a given initial temperature in a PSpice, and suspending circuit simulation when a preset step length of data exchange is reached;

step 2, calculating a power loss data by adopting a power loss calculation method in a MATLAB, and transmitting power loss data into a COMSOL;

step 3, performing a heat-force simulation in the COMSOL, and suspending heat-force simulation when the preset step length of data exchange is reached;

step 4, feeding back an extracted parameter of a junction temperature to a circuit model of the PSpice by the MATLAB; and taking the parameter of junction temperature as a new initial value, and continuing to perform simulation of a next time step length of data exchange based on a former state;

step 5, taking a state when a former loop is terminated as the initial state of a next loop, iterating to perform dynamic continuous multi-physics simulation, and terminating co-simulation when an iteration termination condition is met;

wherein the multi-physics co-simulation method of the power semiconductor module further comprises: enabling a time step length of data exchange of the PSpice and the COMSOL to be equal to the time step length of data exchange of the COMSOL and the PSpice; and setting different time step lengths of data exchange to control a rate of the circuit simulation and a rate of the heat-force simulation, and performing multi-rate multi-physics coupling simulation;

the step of setting the different time step lengths of data exchange comprises the following steps:

constructing a first-order variable step length three-point numerical differentiation formula based on a Lagrange function by extracting and iterating numerical solutions of temperature coupling state variables of nodes, and calculating and obtaining a first-order derivative of an interpolation function of a current node:

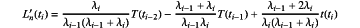wherein t_i−2, t_i−1, t_irepresent three adjacent continuous data exchange time points; t_irepresents a current time node; the relational expressions: t_i−1=t_i−2+λ_i−1, and t_i=t_i−2+λ_i_⁻¹+λ_iare met; T(t_i−2), T(t_i−1) and T(t_i) represent corresponding numerical solutions of temperature at t_i−2, t_i−1, t_i; and λ_iand λ_i_⁻¹represent time step lengths;

a step length adjustment strategy is established according to the first-order derivative of the interpolation function of the current node; and a step length decision interval is set as [ε₁, ε₂], and step length adjustment coefficients are set as a and b respectively, wherein a∈(0,1), b∈(1,+∞), and the following conditions are met:

(1) if |L′_n(t_i)|∈[ε₁, ε₂], λ_i_⁺¹=λ_i;

(2) if |L′_n(t_i)|≤ε₁, λ_i+1=λ_i×b; and a time step length of data exchange is appropriately increased; and

(3) if |L′_n(t_i)|≥ε₂, λ_i+1=λ_i×a; and a step length is decreased.