US 11,777,321 B1
Online estimation of POI-level aggregated inertia considering frequency spatial correlation
Tianshu Bi, Beijing (CN); Cheng Wang, Beijing (CN); Jiahao Liu, Beijing (CN); and Guoyi Xu, Beijing (CN)
Assigned to NORTH CHINA ELECTRIC POWER UNIVERSITY, Beijing (CN)
Filed by NORTH CHINA ELECTRIC POWER UNIVERSITY, Beijing (CN)
Filed on Mar. 2, 2023, as Appl. No. 18/116,685.
Int. Cl. H02J 3/38 (2006.01)
CPC H02J 3/381 (2013.01) [H02J 2300/28 (2020.01)] 1 Claim
OG exemplary drawing
 
1. A method for maintaining power system stability comprising:
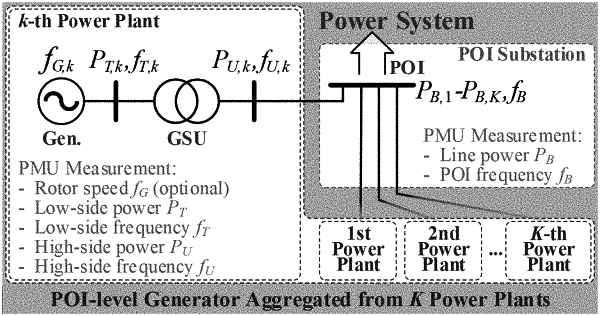
collecting system topology data, reactance values and resistance values of transmission lines from an SCADA/EMS system;
collecting frequency and active power samples from phaser measurement units (PMU) installed at point of interconnection (POI) buses;
calculating active power PT at an POI-level aggregated generator terminal and the rotor speed fG of the POI-level aggregated generator according to the following:

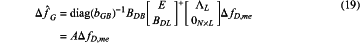OG Complex Work Unit Math
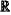where A∈custom characterM×M is a linear correlation between rotor speeds and POI bus frequencies; and
PT=PB,me+diag(r)IB,me2,  (22)
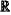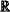where IB,me∈custom characterM×1 and PB,me∈custom characterM×1 are the current and active power of the incoming line measured by the POI-bus PMU, respectively, and diag(r)∈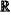custom characterM×M is a diagonal matrix;
if the frequency of POI PMU is not available, adopting (19) under an adjusted PMU combination;
if the non-POI PMUs data are available, calculating the following and obtaining the weighted-least-squares solution fG,W:

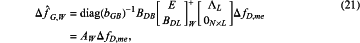OG Complex Work Unit Math
estimating POI-level aggregated inertia by solving the following for each POI bus:
2Ĥagpy(t)=ΔPmu1(t)+u2(t),  (23a)
y={0,fG(t2)−fG(t1),fG(t3)−fG(t1), . . . ,fG(tK)−fG(t1)},  (23b)
ū1={1,1,1, . . . ,1},  (23c)
ū2={0,−PT(t2)+PT(t1),−PT(t3)+PT(t1), . . . ,−PT(tK)+PT(t1)}.  (23d)
in which {Ĥag, ΔPm} is the parameter vector to be identified; y(t) and u2(t) are the values of rotor speed and active power deviation from the operating point,
respectively; and u1(t) represents the mechanical power and remains constant;
estimating the system-level inertia by:

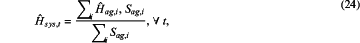OG Complex Work Unit Math
where Ĥag,i and Sag,i are the POI-level aggregated inertia constant and rated capacity of generator i, respectively;
estimating frequency stability indexes including post-disturbance rate of change of frequency (RoCoF) and frequency nadir based on the system-level inertia;
determine whether the frequency stability indexes reach a predetermined limitation;
when the predetermined limitation is reached, activate at least one generator to increase system inertia.