| CPC B25J 9/163 (2013.01) [B25J 9/161 (2013.01); G05B 6/02 (2013.01); G05B 13/027 (2013.01)] | 1 Claim |
|
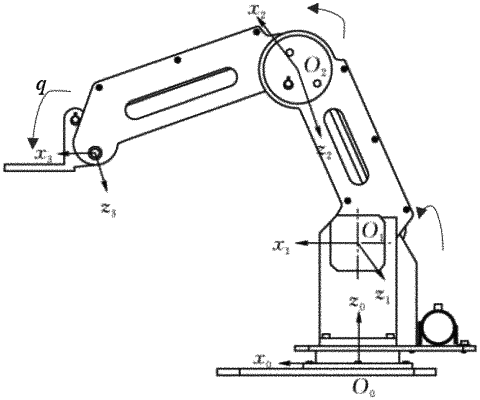
1. A neural network adaptive tracking control method for joint robots, comprising:
1) Establishing a joint robot system model:
Dq(q)q+Cq(q,q)q+Gq(q)+τ(q,t)=ua
in the model mentioned above, q represents a position vector of the joint robot, q represents a velocity vector of the joint robot, q represents an acceleration vector of a joint robot action, ua represents a control input of the joint robot system, the system parameter Dq(q) represents an inertia matrix of the joint robot system, the system parameter Cq(q, q) represents a centrifugal matrix of the joint robot system, the system parameter Gq(q) represents a universal gravitation matrix of the joint robot system, and the system parameter τ(q, t) represents uncertainty and interference factors of the joint robot system;
2) establishing a state space expression and an error definition when taking into consideration both a drive failure and actuator saturation of the joint robot system:
ua(t)=ρ(t)[Γ(0)+L(ξ)ν+ε(ν)]+ε(t)=ρ(t)L(ξ)ν+[ρ(t)Γ(0)+ρ(t)ε(ν)+ε(t)]
e=x1−q*
ë=x1−q*=Dq−1(q)ρ(t)L(ξ)ν+Dq−1(q)[ρ(t)Γ(0)+ρ(t)ε(ν)+ε(t)]+F(⋅)+Q(x1,t)−q*
in the above formulas, ua(t) represents a system control input signal considering both drive failure and actuator saturation, Γ(0)+L(τ)ν+ε(ν) represents a control signal in a case of actuator saturation, wherein ν represents an actual controller design quantity of the system, Γ(0)+L(ξ)ν represents a smooth function proposed according to a mean value theorem of ν, Γ(0) is a bounded matrix, L(ξ) is a non-negative positive definite matrix, ε(ν) is a bounded approximate error and represents an uncertain factor of a controller; ρ(t) represents a health coefficient of a driver, ε(t) represents an interference factor of the driver; e(or e(⋅)) represents a dynamic error of the system (e(⋅) is written as e for simplification in subsequent derivation), ë represents the second derivative of the dynamic error, wherein x1=q represents a motion trajectory of the joint robot, x1 represents an acceleration of the joint robot motion, q* represents a given joint tracking trajectory; q* represents an acceleration of the given joint tracking, F(⋅)=−Dq−1(q) (Cq(q)q+Gq(q), and Q(x1, t)=−Dq−1(q)τ(q, t);
3) designing a proportion integration differentiation (PID) controller and updating algorithms of the joint robot system:
the PID controller ν is expressed as
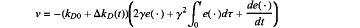 wherein γ is a predetermined parameter, and kD0 is a constant;
wherein the updating algorithms consist of two algorithms as follows:
(1) algorithm based on a robust adaptive control:
the robust adaptive algorithm is designed for automatically updating the controller parameters at an updating rate of:
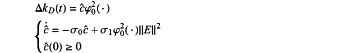 wherein, σ0 and σ1 are positive constants;
 wherein ĉ is an estimated value of c;
a1=max {γdaf, γdγ2, 2γdγ,γdx2}, φ1(⋅)=φf(⋅)+∥e∥+∥ė∥+1, wherein afφf(⋅) is a product of a constant af and a scalar function φf (⋅), representing the upper bound of the system uncertainty factor Dq−1(q)[ρ(t)Γ(0)+ρ(t)ε(ν)+ε(t)]+F(⋅)+Q(x1, t)−q*, x2 is the upper bound of an second derivative q* of a given joint motion trajectory, γd is the upper bound of an system parameter Dq(q), and it is set that
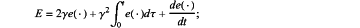 (2) algorithm based on a neural adaptive control:
the neural adaptive algorithm is designed for automatically updating the controller parameters at an updating rate of:
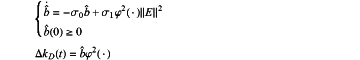 wherein: θ0 and θ1 are positive constants;
Ψ(⋅)=∥S(⋅)∥+1, wherein S(⋅) is a primary function of a neural network; b=max{∥WT∥, m}, wherein b is an estimated value of b, WT is an ideal unknown weight, and m is the upper limit of an reconstruction error ∥η(⋅)∥ of the model;
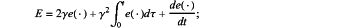 4) controlling trajectory motion of the joint robot by using the PID controller and the updating algorithms designed in step 3) for the joint robot system.
|