	US 12,032,889 B2
	Fast effective resistance estimation using machine learning regression algorithms
Jong Beom Park, Mountain View, CA (US)
Assigned to Synopsys, Inc., Sunnyvale, CA (US)
Filed by Synopsys, Inc., Mountain View, CA (US)
Filed on Mar. 2, 2021, as Appl. No. 17/190,336.
Claims priority of provisional application 62/984,213, filed on Mar. 2, 2020.
Prior Publication US 2021/0271994 A1, Sep. 2, 2021
Int. Cl. G06F 30/36 (2020.01); G06F 18/23213 (2023.01); G06F 30/373 (2020.01); G06F 30/39 (2020.01); G06N 7/00 (2023.01); G06N 20/10 (2019.01); G06F 119/06 (2020.01); G06N 20/00 (2019.01)

CPC G06F 30/36 (2020.01) [G06F 30/373 (2020.01); G06F 30/39 (2020.01); G05B 2219/45028 (2013.01); G06F 18/23213 (2023.01); G06F 2119/06 (2020.01); G06N 7/00 (2013.01); G06N 20/00 (2019.01); G06N 20/10 (2019.01)]

20 Claims

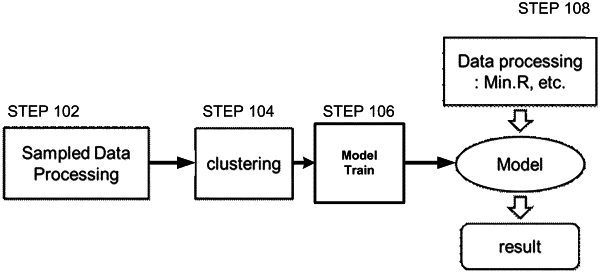
1. A method for estimating/predicting effective resistance between points within an integrated circuit design, the method comprising:

a) determining ratios of a minimum path resistance to an effective path resistance;

b) clustering the ratios into classes using kernel density estimation;

c) training a plurality of regression models for the resulting classes, wherein the regression models include a random forest regression model, a K-nearest neighbor regression model and a linear regression model; and

d) using the random forest regression model, the K-nearest neighbor regression model, and the linear regression model to select which of the random forest regression model, the K-nearest neighbor regression model, and the linear regression model is best with regard to accuracy and recall scores.