US 12,032,602 B2
Scalable topological summary construction using landmark point selection
Gurjeet Singh, Palo Alto, CA (US); Lawrence Spracklen, Boulder Creek, CA (US); and Ryan Hsu, San Francisco, CA (US)
Assigned to SymphonyAI Sensa LLC, Palo Alto, CA (US)
Filed by SymphonyAI Sensa LLC, Palo Alto, CA (US)
Filed on Jul. 22, 2022, as Appl. No. 17/814,499.
Application 17/814,499 is a continuation of application No. 16/286,340, filed on Feb. 26, 2019, granted, now 11,397,753.
Application 16/286,340 is a continuation of application No. 15/147,821, filed on May 5, 2016, granted, now 10,216,828.
Application 15/147,821 is a continuation in part of application No. 14/884,511, filed on Oct. 15, 2015, granted, now 10,002,180.
Application 14/884,511 is a continuation in part of application No. 14/639,954, filed on Mar. 5, 2015, granted, now 10,042,959.
Claims priority of provisional application 62/157,405, filed on May 5, 2015.
Claims priority of provisional application 61/948,490, filed on Mar. 5, 2014.
Prior Publication US 2022/0391415 A1, Dec. 8, 2022
This patent is subject to a terminal disclaimer.
Int. Cl. G06F 16/28 (2019.01); G06F 16/29 (2019.01); G06F 16/901 (2019.01); G06Q 10/0835 (2023.01); G16B 5/00 (2019.01); G16B 40/00 (2019.01)
CPC G06F 16/285 (2019.01) [G06F 16/29 (2019.01); G06F 16/9024 (2019.01); G06Q 10/08355 (2013.01); G16B 5/00 (2019.02); G16B 40/00 (2019.02)] 18 Claims
OG exemplary drawing
 
1. A method comprising:
receiving a first number of data points;
determining at least one size of a plurality of subsets of the first number of data points based on at least one computational constraint, each data point of the first number of data points being a member of at least one of the plurality of subsets of the first number of data points;
transferring each of the plurality of subsets of the first number of data points to a respective one of a plurality of computation devices;
for each of the plurality of subsets of the first number of data points by an associated computation device of the plurality of computation devices:
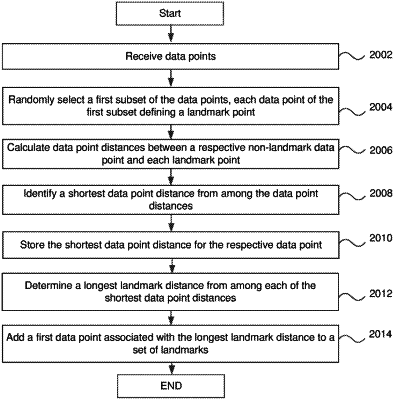
selecting, by the associated computation device, a group of data points from the subset of the first number of data points to generate a first sub-subset of landmarks; and
adding, by the associated computation device, non-landmark data points of the subset of the first number of data points to the first sub-subset of landmarks to create an expanded sub-subset of landmarks, adding the non-landmark data points comprising:
calculating first data point distances between each non-landmark data point and each landmark;
identifying a shortest data point distance from among the first data point distances for each non-landmark data point;
identifying a particular non-landmark data point with a longest first landmark distance of all the shortest data point distances; and
adding the particular non-landmark data point to the first sub-subset of landmarks to expand the first sub-subset of landmarks to generate an expanded set of landmarks, and until the expanded sub-subset of the expanded set of landmarks reaches a predetermined number of members, repeating adding the non-landmark data points;
creating an analysis landmark set based on a combination of expanded sub-subsets of expanded set of landmarks, the analysis landmark set being more computationally efficient based on the at least one computational constraint while maintaining relationships within the first number of data points;
providing the analysis landmark set for analysis;
performing a similarity function on the analysis landmark set to map landmarks of the analysis landmark set to a mathematical reference space;
generating a cover of the mathematical reference space to divide the mathematical reference space into overlapping subsets; and
clustering the mapped landmarks of the analysis landmark set based on the overlapping subsets of the cover in the mathematical reference space.