| CPC G01N 21/3563 (2013.01) [G01N 21/359 (2013.01); G01N 21/8507 (2013.01); G01N 33/24 (2013.01); G01S 19/26 (2013.01); G01N 2021/855 (2013.01); G01N 2201/0636 (2013.01); G01N 2201/0638 (2013.01); G01N 2201/08 (2013.01)] | 19 Claims |
|
1. A method for mapping distribution of chemical compounds in soil, the method comprising the steps of:
inserting a probe into the soil at multiple locations;
utilizing a global navigation satellite system to record the locations of the probe;
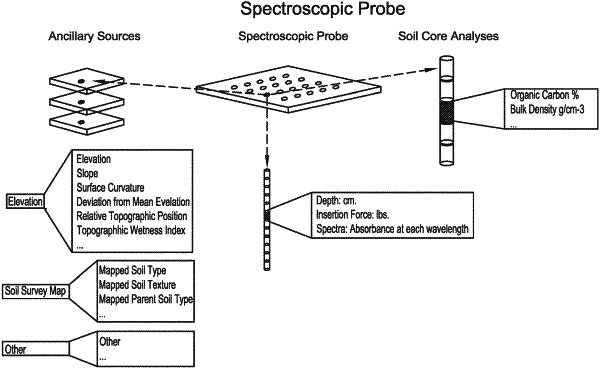
measuring a depth the probe was inserted into the soil for at least two of the multiple locations;
measuring a pressure at which the probe was inserted into the soil for at least two of the multiple locations;
obtaining spectroscopic data regarding the soil;
determining at least one of the group consisting of elevation, slope, surface curvature, relative topographic position, and topographic wetness index of the soil;
determining at least one of the group consisting of soil type, soil texture, and parent material type;
sampling a core of soil adjacent to the probe locations;
dividing the core into multiple depth increments;
analyzing the core;
matching each core with a corresponding depth increment of the probe insertions;
obtaining probe insertion data from the probe insertions;
dividing the probe insertion data into training, validation, and test categories;
resampling spectral variables from the probe insertion data to a wavelength interval longer than a native wavelength interval of an associated spectrometer;
normalizing the probe insertion data on a spectrum by spectrum basis, utilizing a machine learning normalization algorithm, wherein the machine learning normalization algorithm is either a standard normal variate or a Savitzky-Golay algorithm;
standardizing the spectral variables to a common scale by removing a mean and scaling to unit variance;
reducing the number of spectral variables using a Recursive Feature Elimination algorithm with cross-validation and support vector regression;
generating all possible combinations of spectral normalization, regressors, and regressor parameters;
evaluating each of the combinations using five-fold cross validation;
choosing the combination yielding a lowest root mean square error of cross-validation; and
choosing a model utilizing a test set.
|