| CPC B29C 64/393 (2017.08) [B33Y 50/02 (2014.12); G06F 30/10 (2020.01); G06F 2113/10 (2020.01)] | 5 Claims |
|
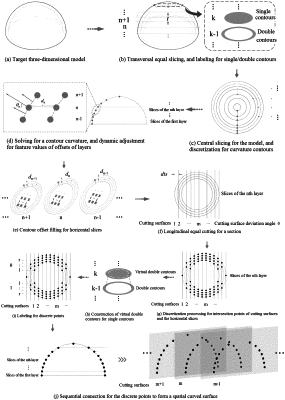
1. A path planning method based on dynamic contour offset discretization and for spatial curved-surface printing, comprising the following steps:
step 1: identifying shape features of a target model, wherein the shape features comprise spatial length, width, and height boundary feature information of the model;
step 2: setting a feature layer thickness value t of transversal equal slicing, carrying out equal slicing on the target model in a height direction from bottom to top by the value t, and sequentially labeling slices as a “slice 1”, a “slice 2”, . . . , a “slice n”, . . . , wherein the feature layer thickness value is a target printing layer thickness value, which is a curved-surface printing layer thickness;
step 3: classifying and identifying the number of contour boundaries for the slices, and labeling critical slices with double/single contours, wherein the last double contour belongs to a “slice k−1”, and the first single contour belongs to a “slice k”, and from bottom to top, sequentially labeling the slices as a “slice 1”, a “slice 2”, . . . , a “slice k−1”, a “slice k”, . . . , a “slice n”, . . . ;
step 4: carrying out central slicing on the target model, carrying out contour intersection with the horizontal slices in the steps 2 to 3 to obtain discrete points of a contour curve of the model, obtaining contour curvature information of the model, and from bottom to top, sequentially labeling the discrete points as a “discrete point 1”, a “discrete point 2”, . . . , a “discrete point n”, . . . in a manner of corresponding to the label numbers of the slices;
step 5: connecting the “discrete point n−1” and the “discrete point n” in pairs, calculating an outer normal vector of a perpendicular bisector of the “discrete point n−1” and the “discrete point n” within a central slicing surface, assigning information of the vector to the “discrete point n−1”, and repeating to obtain uncorrected normal directions of the discrete points; carrying out vector synthesis on the normal directions of the two points “discrete point n−1” and “discrete point n+1” in front of and behind the “discrete point n” to obtain approximately real corrected normal directions of the discrete points; and solving outer deflection angles between the normal directions of the discrete points within the central slicing surface and the horizontal slices where the points are located, and from bottom to top, sequentially labeling the outer deflection angles as a “deflection angle theta 1”, a “deflection angle theta 2”, . . . , a “deflection angle theta n”, . . . in a manner of corresponding to the label numbers of the slices;
step 6: on the basis of the solved contour curvature information of an outer surface in the step 5, solving feature values dn=t/cos(theta n) of contour offsets of the horizontal slices, and realizing dynamic adjustment for the feature values of the contour offsets of the layers;
step 7: according to the labels of the double/single contours in the steps 2 to 3, carrying out equidistant offset filling on the double contours from inner contours to the outside, carrying out equidistant offset filling on the single contours from the outside to the inside, determining the feature values dn of the contour offsets of the layers in the step 6, and from the outside to the inside, sequentially labeling the contours as a “contour 1”, a “contour 2”, . . . , a “contour j”, . . . ;
step 8: setting a longitudinal equal cutting distance dis for a section, carrying out longitudinal cutting for the section on the target model within a width direction range by the value dis, from left to right, sequentially labeling cutting surfaces as a “cutting surface 1”, a “cutting surface 2”, . . . , a “cutting surface m”, . . . , and enabling the longitudinal cutting surfaces to be intersected with the horizontal slices which are subjected to the dynamic contour offset filling in the step 7 to obtain spatial discrete points of the target model;
step 9: according to the labels of the double/single contours in the steps 2 to 3, constructing virtual double contours for the slices with the single contours, and within a series of the cutting surfaces containing the single contours, on the basis of a distance ratio of the inner/outer boundary discrete points of the critical “slice k−1” with the last double contour, selecting the inner discrete points to construct virtual inner contours by taking distances of the outer boundary discrete points of the single contours as the benchmark;
step 10: for the labels of the spatial discrete points of the target model, introducing a relative position variable 0/1, and symmetrically labeling the discrete points within the cutting surfaces, wherein the rule for a starting label “i” of the inner boundary discrete points is “when the slice label is not greater than k−1, the starting label of the inner boundary discrete points is 1, and the subsequent labels continue to increase as the slice label increases”, sequentially labeling the discrete points as “0| . . . ”, “0|r”, “0| . . . ”, “0|i+1”, “0|i”; “1|i”, “1|i+1”, “1| . . . ”, “1|r”, and “1| . . . ”;
step 11: on the basis of the above steps 1 to 10, discretizing a three-dimensional spatial equidistant lattice [n, j, m, 0/1, r] for the target model, and independently labeling any one discrete point, with unrepeated labeling information; and
step 12: sequentially connecting the discrete points labeled with the same value r within a single cutting surface to obtain a spatial curve within the single cutting surface; under the labeling with the same value r, connecting the spatial curves within the cutting surfaces end to end in the order of the value m of the section to obtain single-layer spatial curved surfaces; and connecting the single-layer spatial curved surfaces end to end in the order of the value r, and stacking layer by layer to obtain an overall spatial curved-surface path of the target model.
|