| CPC G01M 7/02 (2013.01) [G01B 21/32 (2013.01); G01M 15/14 (2013.01); G06F 30/23 (2020.01)] | 4 Claims |
|
1. A non-contact dynamic strain field measuring method for a rotating blade, comprising the following steps:
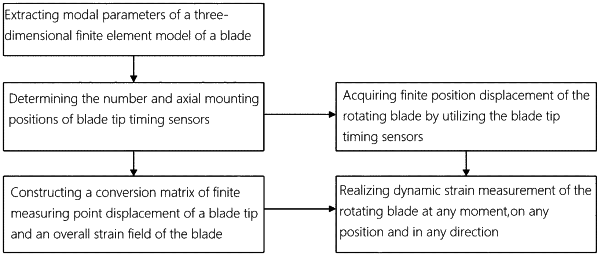
in the first step (S1), determining a to-be-measured rotating blade, and establishing a three-dimensional finite element model of the to-be-measured rotating blade, and extracting modal parameters of the three-dimensional finite element model, in the first step S1, first nm order modal parameters: a modal frequency fi, a displacement modal shape ϕi with the size being ndof×1 and a strain modal shape ψi with the size being 2ndof×1, of the three-dimensional finite element model are extracted by modal analysis, and a full-field displacement modal shape matrix, Φ=[ϕ1, ϕ2, . . . , ϕnm] with the size being ndof×nm, of the rotating blade and a full-field strain modal shape matrix, ψ=[ψ1, ψ2, . . . , ψnm] with the size being 2ndof×nm, of the rotating blade are constructed, wherein nm represents for a modal number, i represents for a modal order, ndof represents for the number of degrees of freedom of the finite element model of the rotating blade, ndof=3nn, and nn represents for the number of nodes of the finite element model of the rotating blade;
in the second step (S2), determining the number and axial mounting positions of blade tip timing sensors, wherein a measuring point selection matrix Φp=[ϕ′1, ϕ′1, . . . , ϕ′nm] is constructed based on a displacement modal shape capable of mounting the blade tip timing sensors of the rotating blade, nd measuring points are randomly selected from the measuring point selection matrix Φp to construct a measuring point displacement modal shape matrix Φd with the size being nd×nm, the condition number κ of the matrix is calculated, a random process is repeated for R times, and a measuring point layout when the condition number κ of the matrix is minimum is selected therefrom; the number nd of axial blade tip timing measuring points of the rotating blade is not be smaller than the number nm of concerned modes, namely nd≥nm; in a solution, first three order vibration modes of the simulated rotor blade are concerned, and nm=3; the number of the blade tip timing sensors is minimized, namely nd=3, thus yielding a minimized number of the blade tip timing sensors;
in the second step S2, a displacement modal shape capable of mounting the blade tip timing sensors in an axial direction of a blade tip of the blade is extracted, wherein nc represents for the number of finite element grid nodes of the blade tip of the blade, and each node selects a circumferential displacement modal shape;
in the third step (S3), constructing a conversion matrix of finite measuring point displacement and an overall strain field, wherein in the third step S3, a conversion matrix T=ψΦd† with the size being 2ndof×nd is constructed, wherein Φd†=[ΦdTΦd]−1ΦdT represents for an inversion of the measuring point displacement modal shape matrix Φd;
in the fourth step (S4), disposing the minimized number of the blade tip timing sensors close to an inner side of the casing; performing displacement measurement by a blade tip timing vibration measuring module connected with the minimum number of the blade tip timing sensors and acquiring blade tip finite position displacement of the rotating blade based on the blade tip timing sensors, wherein displacement signals u(t)=[u1(t), u2(t), . . . , und(t)]T on nd positions in an axial direction of the rotating blade within t moments are acquired by a blade tip timing non-contact measuring system; and
in the fifth step (S5), acquiring, by a dynamic strain, dynamic strains of the rotating blade at any moment, on any position and in any direction based on modal processing of the conversion matrix, wherein in the fifth step (S5), based on the conversion matrix T and the displacement signals u(t) measured by blade tip timing, strains of all nodes on a surface of and inside the rotating blade within the t moment are calculated according to a formula S(t)=Tu(t) to obtain S(t)=[ε1,x,ε1,y,ε1,z,γ1,xy,γ1,yz,γ1,xz, . . . , εi,x,εi,y,εi,z,γi,xy,γi,yz,γi,xz, . . . , εnn,x,εnn,y, εnn,z,γnn,xy,γnn,yz,γnn,xz]T, and the strains S(t) comprise positive strains and shearing strains, wherein εi,x represents for a positive strain of the ith node of the finite element model of the blade in an x direction, εi,y represents for a positive strain of the ith node of the finite element model of the blade in a γ direction, εi,z represents for a positive strain of the ith node of the finite element model of the blade in a z direction, γi,xy represents for a shearing strain of the ith node of the finite element model of the blade in an x-y direction, γi,yz represents for a shearing strain of the ith node of the finite element model of the blade in a y-z direction, and γi,xz represents for a shearing strain of the ith node of the finite element model of the blade in an x-z direction, thus realizing reconstruction of the overall strain field of the rotating blade by only utilizing the blade tip finite measuring point displacement, wherein not only is the measurement of the dynamic strain on the surface of the blade realized, but also the measurement of the positive strains and the shearing strains of the nodes inside the blade is realized;
wherein a plurality of blade tip timing sensors are arranged on the casing; a blade tip timing vibration measuring module connected with the blade tip timing sensors so as to measure displacement signals u(t)=[u1(t), u2(t), . . . , und(t)]T on nd positions in an axial direction of the rotating blade within t moments; and
a strain field reconstruction module configured to calculate the strains of all the nodes on the surface of and inside the rotor blade within t moments according to a formula S(t)=Tu(t) to obtain S(t)=[ε1,x,ε1,y,ε1,z,γ1,xy,γ1,yz,γ1,xz, . . . , εi,x,εi,y,εi,z,γi,xy,γi,yz,γi,xz, . . . , εnn,x,εnn,y, εnn,z,γnn,xy,γnn,yz,γnn,xz]T,
wherein the strains S(t) include positive strains and shearing strains, thus reconstructing dynamic strains of all the nodes on the surface of and inside the rotating blade and enhancing reliability of obtaining dynamic strains of the with the rotating blade finite positions of finite blades with the minimum number of the blade tip timing sensors.
|