| CPC G06Q 10/04 (2013.01) [G06Q 10/06315 (2013.01)] | 20 Claims |
|
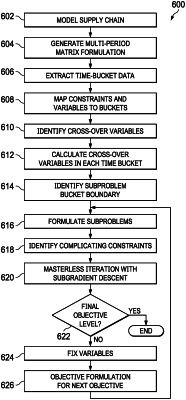
1. A system for iteratively solving a supply chain demand planning problem modeled as a linear programming (LP) problem, comprising:
a computer, comprising a processor and memory, the computer configured to:
receive a multi-period matrix formulation of at least a portion of an LP supply chain demand planning problem;
map constraints of the LP supply chain demand planning problem and variables of the LP supply chain demand planning problem to a planning horizon;
formulate at least two time-based decomposed subproblems by decomposing the LP supply chain demand planning problem at one or more decomposition boundaries;
identify complicating constraints;
perform masterless iteration with subgradient descent; and
repeat the formulate, identify and perform to incrementally improve an overall solution until a stopping criteria is met.
|