	US 11,954,456 B2
	Float division by constant integer
Jonas Kallen, Hisings Backa (SE); and Sam Elliott, London (GB)
Assigned to Imagination Technologies Limited, Kings Langley (GB)
Filed by Imagination Technologies Limited, Kings Langley (GB)
Filed on Apr. 27, 2023, as Appl. No. 18/140,571.
Application 18/140,571 is a continuation of application No. 17/547,071, filed on Dec. 9, 2021, granted, now 11,645,042.
Application 17/547,071 is a continuation of application No. 16/548,359, filed on Aug. 22, 2019, granted, now 11,294,634, issued on Apr. 5, 2022.
Claims priority of application No. 1813701 (GB), filed on Aug. 22, 2018.
Prior Publication US 2023/0297338 A1, Sep. 21, 2023
Int. Cl. G06F 7/556 (2006.01); G06F 7/487 (2006.01); G06F 7/72 (2006.01)

CPC G06F 7/556 (2013.01) [G06F 7/4873 (2013.01); G06F 7/727 (2013.01)]

20 Claims

1. A binary logic circuit for determining the ratio x/d where x is a variable integer input of w bits comprising M>8 blocks of bit width r≥1 bit, and d>2 is a fixed integer, the binary logic circuit comprising:

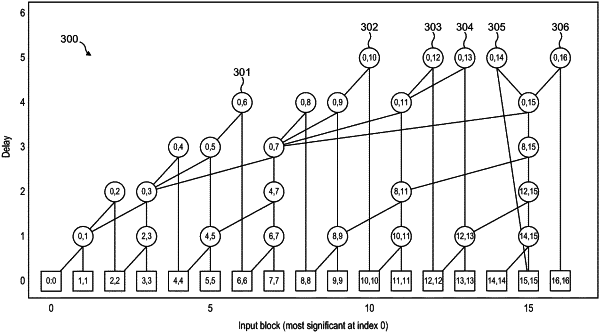
a logarithmic tree of modulo units each configured to calculate x[a: b]mod d for respective block positions a and b in x where b>a with the numbering of block positions increasing from the most significant bit of x up to the least significant bit of x, the modulo units being arranged such that a subset of M−1 modulo units of the logarithmic tree provide x[0:m]mod d for all m∈{1, M−1}, and, on the basis that any given modulo unit introduces a delay of 1, all of the modulo units are arranged in the logarithmic tree within a delay envelope of [log₂M]; and

output logic configured to combine the outputs provided by the subset of M−1 modulo units with blocks of the input x so as to yield the ratio x/d;

wherein the total number of modulo units T in the logarithmic tree for a given number of blocks M is in accordance with the following table:


	M	T

	24	46
	25	48
	26	51
	27	54
	28	58
	29	61
	30	65
	31	69
	32	74
	33	60
	34	62
	35	64
	36	67
	37	69
	38	72
	39	74
	40	78
	41	80
	42	83
	43	85
	44	89
	45	91
	46	94
	47	96
	48	101
	49	103
	50	106
	51	109
	52	113
	53	116
	54	120
	55	123
	56	128
	57	131
	58	135
	59	139
	60	144
	61	148
	62	153
	63	158
	64	164
	65	133
	66	135
	67	137
	68	140
	69	142
	70	145
	71	147
	72	151
	73	153
	74	156
	75	158
	76	162
	77	164
	78	167
	79	169
	80	174
	81	176
	82	179
	83	181
	84	185
	85	187
	86	190
	87	192
	88	197
	89	199
	90	202
	91	206
	92	210
	93	214
	94	217
	95	219
	96	225
	97	227
	98	230
	99	233
	100	237
	101	240
	102	244
	103	247
	104	252
	105	255
	106	259
	107	262
	108	267
	109	270
	110	274
	111	277
	112	283
	113	286
	114	290
	115	294
	116	299
	117	303
	118	308
	119	313
	120	319
	121	323
	122	328
	123	333
	124	339
	125	344
	126	350
	127	356
	128	363.