	US 11,953,903 B2
	Neural network-based method for calibration and localization of indoor inspection robot
Yongduan Song, Chongqing (CN); Jie Zhang, Chongqing (CN); Junfeng Lai, Chongqing (CN); Huan Liu, Chongqing (CN); Ziqiang Jiang, Chongqing (CN); and Li Huang, Chongqing (CN)
Assigned to Chongqing University, Chongqing (CN); Star Institute of Intelligent Systems, Chongqing (CN); and DB (Chongqing) Intelligent Technology Research Institute Co., LTD, Chongqing (CN)
Filed by CHONGQING UNIVERSITY, Chongqing (CN); STAR INSTITUTE OF INTELLIGENT SYSTEMS, Chongqing (CN); and DB (CHONGQING) INTELLIGENT TECHNOLOGY RESEARCH INSTITUTE CO., LTD., Chongqing (CN)
Filed on Jan. 31, 2022, as Appl. No. 17/589,179.
Claims priority of application No. 202110448691.1 (CN), filed on Apr. 25, 2021.
Prior Publication US 2022/0350329 A1, Nov. 3, 2022
Int. Cl. G05D 1/00 (2006.01); G06N 3/084 (2023.01); H04B 17/318 (2015.01)

CPC G05D 1/0088 (2013.01) [G05D 1/0272 (2013.01); G05D 1/028 (2013.01); G06N 3/084 (2013.01); H04B 17/318 (2015.01); G05D 2201/0207 (2013.01)]

4 Claims

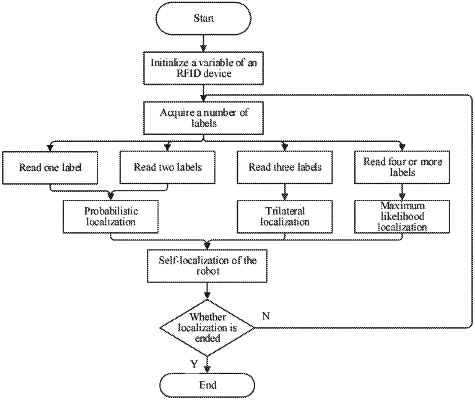
1. A neural network-based method for calibration and localization of an indoor inspection robot, comprising the following steps:

S100: presetting indoor positions for N label signal sources, the label signal sources being capable of transmitting radio frequency (RF) signals;

S200: providing a reader-writer for receiving the signals of the label signal sources on an indoor robot, and computing, during an indoor traveling process of the robot, an actual path of the robot according to numbers of signal labels received by the reader-writer at different moments, specifically:

S210: establishing a log-normal propagation loss model according to a signal strength of received labels:

P(d)=P(d₀)−10α log(d/d₀)−X_σ (2-1)

wherein, P(d) represents a signal strength from labels received by a reader, P(d₀) represents a signal strength from labels received by the reader at a reference point d₀, α represents a scale factor between a path length and a path loss, X_σ represents a Gaussian random variable having an average of 0, d₀represents a distance from the reference point to each of the labels, and d represents a distance from a label to be computed to the reader;

S220: obtaining a distance d from each of the label signal sources to the reader-writer by transforming eq. (2-1):

d=10^[P(d^₀^)-P(d)]/10α (2-2)

wherein, P(d₀) represents a signal strength at 1 m, and α represents a signal propagation constant;

S230: randomly selecting I moments within a time interval T, and assuming that a number of label signals received by the reader-writer at a t^thmoment is n, then computing an actual coordinate of the robot at the t^thmoment as:

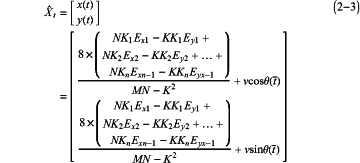wherein,

E_x1=x₁−x_n,E_x2=x₂−x_n, . . . ,E_xn-1=x_n-1−x_n;

E_y1=y₁−y_n,E_y2=y₂−y_n, . . . ,E_yn-1=y_n-1−y_n;

K=(x₁−x_n)(y₁−y_n)+(x₂−x_n)(y₂−y_n)+ . . . +(x_n-1−x_n)(y_n-1−y_n);

K₁=x₁²−x₄²+y₁²−y₄²+d₄²−d₁²;

K₂=x₂²−x₄²+y₂²−y₄²+d₄²−d₂²;

K_n=x_n-1²−x_n²+y_n-1²−y_n²+d_n²−d_n-1²;

M=(x₁−x₄)²+(x₂−x₄)²+. . . +(x_n-1−x_n)²;

N=(y₁−y₄)²+(y₂−y₄)²+. . . +(y_n-1−y_n)²;

S240: establishing a model with coordinates of the robot in the I moments to obtain an actual path of the robot:

RSSI={RSSI_x,RSSI_y}={x₁′,x₂′, . . . ,x_n′,y₁′,y₂′, . . . ,y_n′} (2-4)

wherein, RSSI={RSSI_x,RSSI_y} represents the actual path of the robot, and RSSI_xand RSSI_yrepresent an x coordinate and a y coordinate computed through RF identification (RFID)-based localization; and

S250: obtaining an actual path of the robot in the I moments with the method in S210-S240;

S300: computing positional information moved by the robot at the t^thmoment:

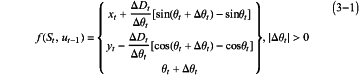wherein, u_t=(ΔD_t,Δθ_t)^Trepresents a pose increment, S_t=(x_t,y_t,θ_t) represents a state of the robot at the t^thmoment, (x,y) represents a coordinate of the robot at the t^thmoment, θ represents a direction angle at the t^thmoment, ΔD_tis an arc length moved by the robot within time Δ_t, and Δθ_tis a change of a direction angle in a pose of the robot within the time Δt;

S400: processing the positional information of the robot at the t^thmoment in step S300 with a generalized linear model (GLM) to obtain a predicted path of the robot at the t^thmoment:

GLM={x₁,x₂, . . . ,x_n,y₁,y₂, . . . ,y_n} (4-1)

wherein, x_{1 . . . n}is an x coordinate of the predicted path estimated by the GLM, and y_{1 . . . n}is a y coordinate of the predicted path estimated by the GLM, thereby obtaining a predicted path corresponding to each moment;

S500: establishing an odometry error model E with the neural network:

E=Σ_n|O−RSSI|² (5-1)

wherein, O represents an optimized predicted path;

S600: presetting a maximum number of iterations, taking the actual path in the I moments and a corresponding predicted path as an input of a neural network model to train the error model E, updating parameters of the model through back propagation (BP) during training, and stopping training when E≤e⁻⁵to obtain a well-trained odometry error model; and

S700: repeating steps S300-S400 to obtain a predicted traveling path of a robot R′ to be predicted, and inputting the predicted traveling path to the well-trained odometry error model in step S600 to obtain an optimized predicted traveling path that is a predicted value for a traveling path of the robot R′.