| CPC G01L 5/04 (2013.01) [G06F 17/11 (2013.01)] | 2 Claims |
|
1. A quasi-static calculation method for lateral unbalanced force of transmission lines, comprising the following steps:
step 1: determining mean wind-induced lateral unbalanced force
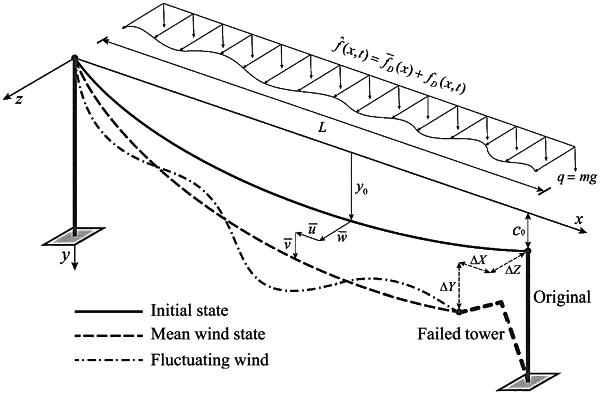
for a span conducting wire with an initial vertical height difference c0 at both ends, displacement components of one end in longitudinal direction (x-axis direction), vertical direction (y-axis direction) and lateral direction (z-axis direction) are respectively ΔX, ΔY and ΔZ, and a standard cubic equation with H1 as a variable is obtained:
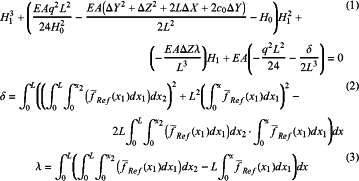 where: H0 represents initial horizontal tension; EA represents Young's modulus; q represents weight per unit length of the span conducting wire; L represents horizontal span; both δ and λ represent constants related to mean wind pressure; fRef(x) is a distribution function of the mean wind pressure along line direction; and H1 represents horizontal tension of the span conducting wire under combined action of support displacement and mean wind, which can be obtained by solving formula (1) via a Cardan's formula;
further, the mean wind-induced lateral unbalanced force at both ends of the span conducting wire is obtained:
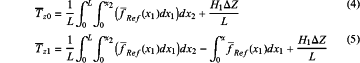 where: subscripts 0 and 1 respectively represent one side of the span conducting wire without support displacement and one side of the span conducting wire with support displacement, the same below;
step 2: determining fluctuating wind-induced lateral unbalanced force
considering quasi-static background response only, the fluctuating wind-induced lateral unbalanced force at both ends of the span conducting wire is calculated by an influence line method:
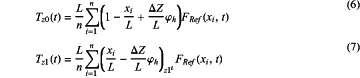 where: FRef(xi,t) represents fluctuating wind load acting on each point of the span conducting wire; n represents number of wind speed simulation points; xi represents x-coordinate of the fluctuating wind load; φh represents increment of horizontal tension caused by unit wind load, and the expression thereof is:
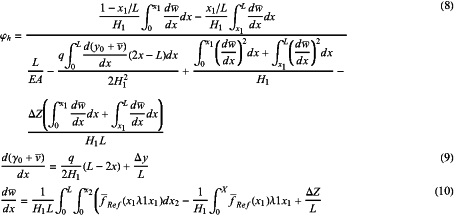 where: y0, v and w respectively represent initial vertical displacement, vertical displacement under combined action of mean wind and support displacement, and lateral displacement caused by mean wind of the span conducting wire;
finally, total lateral reaction force is a sum of the mean wind-induced lateral unbalanced force and the fluctuating wind-induced lateral unbalanced force, the total lateral unbalanced force is obtained:
Tz0(t)=Tz0+Tz0(t) (11)
Tz1(t)=Tz1+Tz1(t) (12).
|