US 11,947,506 B2
Method and system for mapping a dataset from a Hilbert space of a given dimension to a Hilbert space of a different dimension
Seyed Shakib Vedaie, Vancouver (CA); Ehsan Zahedinejad, Vancouver (CA); Roohollah Ghobadi, Vancouver (CA); Daniel J. Crawford, Vancouver (CA); Jaspreet S. Oberoi, Vancouver (CA); Inderpreet Singh, Vancouver (CA); and Moslem Noori, Vancouver (CA)
Assigned to 1QB INFORMATION TECHNOLOGIES, INC., Vancouver (CA)
Filed by 1QB Information Technologies Inc., Vancouver (CA)
Filed on Dec. 16, 2021, as Appl. No. 17/553,551.
Application 17/553,551 is a continuation of application No. PCT/IB2020/055801, filed on Jun. 19, 2020.
Claims priority of provisional application 62/925,488, filed on Oct. 24, 2019.
Claims priority of provisional application 62/863,510, filed on Jun. 19, 2019.
Prior Publication US 2022/0107927 A1, Apr. 7, 2022
Int. Cl. G06F 16/22 (2019.01); G06N 10/40 (2022.01)
CPC G06F 16/22 (2019.01) [G06N 10/40 (2022.01)] 20 Claims
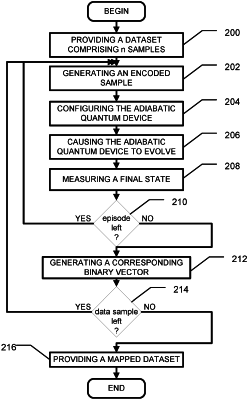
OG exemplary drawing
 
1. A computer-implemented method for mapping a dataset from a Hilbert space of a given dimension to a Hilbert space of a different dimension, the method comprising:
(a) obtaining a dataset D comprising n data samples xi, xi∈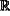custom characterp for i∈{1,2, . . . , n}, wherein p is a dimension of each data sample;
(b) for each of n data samples xi of the dataset D,
(i) for a plurality of episodes e,
(A) generating an encoded sample Ji=Axi+b, wherein A is a q×p matrix comprising elements drawn from a first distribution, wherein q is indicative of a number of qubits available in an adiabatic quantum device, and wherein b is a q-dimensional vector comprising elements drawn from a second distribution;
(B) configuring the adiabatic quantum device by embedding the encoded sample into a q-body Ising Hamiltonian H representative of the adiabatic quantum device and defined by:

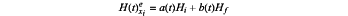OG Complex Work Unit Math
wherein a(t) and b(t) are classical external fields driving a Hamiltonian H(t) over the time span [0,T], wherein Hi is an initial Hamiltonian and Hf is a final or an encoding Hamiltonian defined, respectively, by:

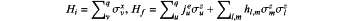OG Complex Work Unit Math
wherein σx, σz are Pauli-X and Pauli-Z operators, respectively, and wherein hl,m is a parameter defined as a function that depends on values ju e of the encoded sample;
(C) causing the adiabatic quantum device to evolve from an initial state at ti=0 to a final state at tf=t wherein t≤T; and
(D) performing a projective measurement along a z axis at the final state to determine a value of each qubit of the number of qubits of the adiabatic quantum device;
(ii) generating a corresponding binary vector representative of each data sample xi in a transformed Hilbert space using the value of each qubit at each episode e determined in (D), wherein the corresponding binary vector corresponds to a mapped data sample; and
(c) providing a mapped dataset comprising each of the corresponding binary vectors generated in (ii).