	US 12,266,942 B1
	Fast-response PV simulator based on improved deadbeat predictive current control
Kejun Li, Jinan (CN); Zhijie Liu, Jinan (CN); Yuanzong Song, Jinan (CN); Zhenshan Huang, Jinan (CN); Yuchuan Li, London (GB); Gang Shen, Jinan (CN); Yuanyuan Sun, Jinan (CN); Kaiqi Sun, Jinan (CN); Jie Lou, Jinan (CN); Liang Zhang, Jinan (CN); and Kehan Zhang, Jinan (CN)
Assigned to SHANDONG UNIVERSITY, Jinan (CN); SHANDONG JIAOTONG UNIVERSITY, Jinan (CN); SHANDONG BEIXINGQUAN ENERGY CO., LTD., Jinan (CN); and IMPERIAL COLLEGE LONDON, London (GB)
Filed by SHANDONG UNIVERSITY, Jinan (CN); SHANDONG JIAOTONG UNIVERSITY, Jinan (CN); SHANDONG BEIXINGQUAN ENERGY CO., LTD., Jinan (CN); and IMPERIAL COLLEGE LONDON, London (GB)
Filed on Nov. 14, 2024, as Appl. No. 18/947,049.
Claims priority of application No. 202311593523.7 (CN), filed on Nov. 27, 2023.
Int. Cl. H02J 3/38 (2006.01); H02P 21/22 (2016.01); H02S 40/32 (2014.01); H02S 50/10 (2014.01)

CPC H02J 3/381 (2013.01) [H02P 21/22 (2016.02); H02S 40/32 (2014.12); H02S 50/10 (2014.12); H02J 2300/26 (2020.01)]

2 Claims

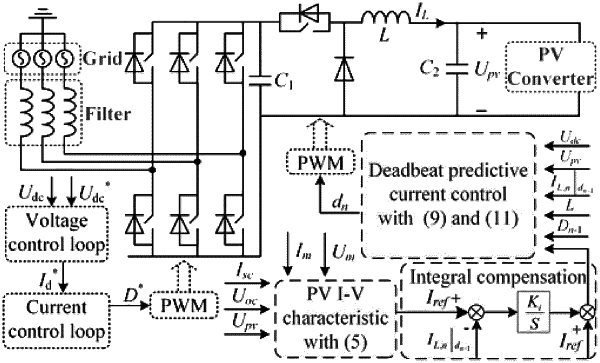
1. A fast-response PV simulator based on an improved deadbeat predictive current control (DPCC), comprising a reference value calculation module, a DPCC controller and a modulation control module, wherein the reference value calculation module is implemented through a PV array model, the PV array model collects the output voltage U_pvin real time, and combines with the set voltage of maximum power point U_m, the set current of maximum power point I_m, short-circuit current I_sc, and open-circuit voltage U_octo calculate the reference value of the output current I_ref,

the DPCC controller receives the calculated reference current value and derives the deadbeat control law for the inductor current by formulating the discrete model of the power electronic converter; it inputs the collected direct current bus voltage U_dc, output voltage U_pv, the current inductor current I_L,n+1|_d_{_n+1}, inductor value L, the previous moment's duty cycle d_n−1and the reference value of current I_refinto DPCC controller to obtain the reference value of duty cycle for the next moment d_n;

the calculated reference value of duty cycle d_nis automatically updated at the start of the next moment; the modulation control module obtains the triggering signals for the Insulated Gate Bipolar Transistor (IGBT) through the modulation sector; after passing through the drive circuit, it performs real-time control of the IGBT, enabling the output current of the fast-response PV simulation to track its reference value;

the implementation steps of the DPCC controller are as follows:

(1) equivalent DC-DC topology of the fast response PV simulation

the DC-DC topology of the fast-response PV simulator can be equivalent to a buck converter for analysis; when the DPCC strategy is used in the DC-DC converter, the inductor current must be accurately modeled to obtain the correct predicted value of the control variable;

when the switch tube is on, the expression of the inductor current is as follows:

where L is the inductance value of the buck converter, I_L1is the value of the inductor current, U_on, is the output voltage of the buck converter, and U_dcis the input voltage;

when the switch tube is off, the expression of the inductor current is as follows:

where U_offis the output voltage of the buck converter, and I_L2is the value of the inductor current;

when the buck converter works in a steady state, the energy of the inductor is balanced between absorption and dissipation during a single switching period. Due to the short duration of a single switching period, the output voltage is considered constant during this interval; therefore, the output voltage of the switch tube does not change in a single switching period, as follows:

U_on=U_off (3)

(2) accurate modeling of inductor current in fast response PV simulation

assume that the value of the inductor current at time t_nis I_L,n; if the duty ratio at time t_nis the same as that at time t_n−1, then, at time t_n+1, the calculation expression for the value of the inductor current is as follows:

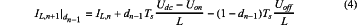where d_n−1is the duty ratio at time t_n−1, I_L,n+1|_d_{_n+1}is the value of the inductor current at time t_n+1when the duty ratio is d_n−1, and T_sis the switching period of the buck converter;

when the duty ratio changes to d_nat time t_n, the value of the inductor current at time t_n+1is expressed as I_L,n+1|_d_{_n};

(3) control law of DPCC

the relationship between I_L,n+1|_d_{_n}and I_L,n+1|_d_{_n+1}is as follows:

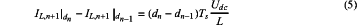equation (5) shows that if the duty ratio changes from d_n−1to d_nat time t_n, then, at time t_n+1, the value of the inductor current will change to I_L,n+1|_d_{_n}, consequently, if the reference value of the inductor current is equal to I_L,n+1|_d_{_n}, the DPCC of the inductor current can be realized; therefore, the DPCC law for the DC-DC topology of the fast-response PV simulator can be presented as follows:

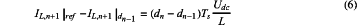where I_L,n+1|_refis the reference value of the inductor current at time t_n+1.