| CPC G06N 10/00 (2019.01) | 20 Claims |
|
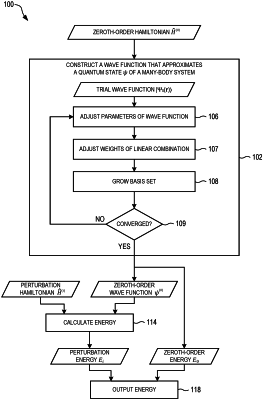
1. A method for determining a perturbation energy of a quantum state of a many-body system, comprising:
constructing a wave function that approximates the quantum state by adjusting parameters of the wave function to minimize an expectation value of a zeroth-order Hamiltonian, wherein:
the zeroth-order Hamiltonian explicitly depends on a finite mass of each of a plurality of interacting quantum particles that form the many-body system;
the quantum state has a non-zero total angular momentum;
the wave function is expressed as a linear combination of explicitly correlated Gaussian basis functions; and
each of the explicitly correlated Gaussian basis functions includes a preexponential angular factor;
calculating a theoretical estimate of the perturbation energy based on the wave function and a perturbation Hamiltonian that explicitly depends on the finite mass of each of the plurality of interacting quantum particles; and
outputting the theoretical estimate of the perturbation energy for use in configuring an apparatus such that the apparatus is capable of performing a measurement of a transition energy of the many-body system, the transition energy being based on the perturbation energy, the measurement of the transition energy having an experimental uncertainty that is equal to or less than the theoretical estimate of the perturbation energy.
|