| CPC G06F 7/588 (2013.01) [G06F 7/523 (2013.01)] | 8 Claims |
|
1. A computer-implemented method, carried out between a plurality of D dealer nodes and N computing nodes, of calculating the result of an arithmetic function ƒ which can be expressed as the addition of A groups of multiplications of a set S of private input secrets {s0, s1, . . . , sS-1} such that:
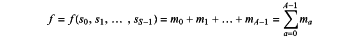 where each group of multiplications ma, a∈{0, 1, . . . , A−1} is the product of Ma secrets of said set S of private input secrets:
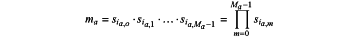 the subindices ia,m for a∈{0, 1, . . . , A−1}, m∈{0, 1, . . . , Ma−1} identify private input secrets from the set of S secrets,
where the S secrets are selected from integers, real numbers or complex numbers,
each secret is known to one of said dealer nodes,
and each computing node operates independently from the other N computing nodes, wherein the method comprises:
a) providing each dealer node contributing a secret sia,m to a group of multiplications ma with a base blinding factor ρa which is common to all secrets contributing to said group of multiplications ma, wherein the base blinding factor ρa satisfies (modulo p, where p is a prime number):
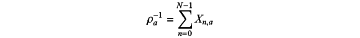 for a set of (N×A) random or pseudorandom numbers Xn,a for n∈{0, 1, . . . , N−1}, a∈{0, 1, . . . , A−1} each associated with a respective one of the N computing nodes;
b) providing each dealer node contributing a secret sia,m to a group of multiplications ma with an exponent blinding factor λa,m which is specific to said secret sia,m, wherein the set of exponent blinding factors λa,m collectively satisfy (modulo p):
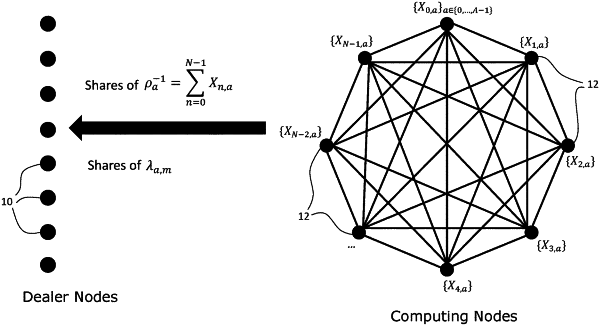
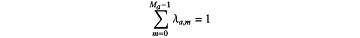 c) storing said set of (N×A) random or pseudorandom numbers Xn,a for n∈{0, 1, . . . , N−1}, a∈{0, 1, . . . , A−1} either (i) at the computing nodes in a first mode of operation (“network mode”) whereby each of the N computing nodes stores a subset of A random or pseudorandom numbers unique to that node, or (ii) at the dealer nodes in a second mode of operation (“edge mode”) whereby each dealer node stores at least the subset of the (N×A) random or pseudorandom numbers Xn,a corresponding to the additions to which that dealer contributes a secret;
d) each dealer node computing, for each secret sia,m, one or more shares for that secret wherein in the network mode of operation a single share is computed, modulo p, as:
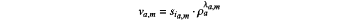 and wherein in the edge mode of operation a plurality of N shares are computed, using the N random or pseudorandom numbers Xn,a associated with the group of multiplications ma to which the secret sia,m contributes, modulo p, as:
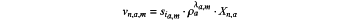 e) each dealer node sending to each of the computing nodes a respective share message which, in the network mode of operation contains the same single share va,m, and in the edge mode of operation contains a respective one of the N shares vn,a,m such that each of the N computing nodes receives the shares indexed to a unique value n∈{0, 1, . . . , N−1};
f) each computing node independently calculating, for the received shares va,m Or vn,a,m associated with each group of multiplications ma, a local product result which in the network mode of operation is calculated, modulo p, as:
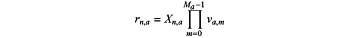 and which in the edge mode of operation is calculated, modulo p, as:
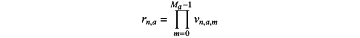 g) each computing node independently calculating a local addition result from the set of local product results, modulo p, as:
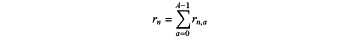 h) receiving the local addition result from each of the N computing nodes; and
i) computing an output of the function ƒ by combining the local addition results from the N computing nodes to compute:
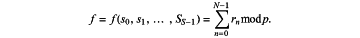 |