| CPC B01L 3/0227 (2013.01) [B01L 3/0237 (2013.01); C12N 15/89 (2013.01); G01N 21/6428 (2013.01); G01N 21/6458 (2013.01); G02B 21/16 (2013.01); G02B 21/26 (2013.01); G02B 21/32 (2013.01); G02B 21/36 (2013.01); G01N 2021/6439 (2013.01)] | 9 Claims |
|
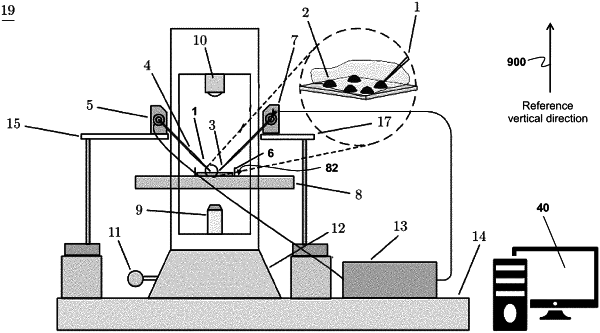
1. A system for automatically providing microinjection of a sample to a plurality of adherent cells, the plurality of adherent cells being disposed on a Petri dish, the system comprising:
a motorized stage for two-dimensionally moving the Petri dish;
a plurality of motorized micromanipulators for manipulating a plurality of micropipettes used for injecting the sample to the plurality of adherent cells, an individual micromanipulator being configured to hold and manipulate a respective micropipette in the plurality of micropipettes;
a gas pressure provider connectable to an individual micropipette for controllably forcing out the sample present in the individual micropipette;
an optical microscope for viewing the Petri dish disposed on the motorized stage;
a camera for capturing a cell image containing the plurality of adherent cells as viewed through the optical microscope; and
one or more computers for controlling the system, the one or more computers being configured to:
control the motorized stage to sequentially visit respective cells in the plurality of adherent cells according to an injection sequence, wherein the injection sequence is an optimized one selected by minimizing a total distance traveled by the motorized stage to sequentially visit the respective cells such that each of the respective cells is visited once by one micropipette selected from the plurality of micropipettes, whereby when the respective cells are randomly distributed on the Petri dish, using the plurality of micropipettes reduces the minimized total distance over using a single micropipette to thereby increase a throughput of microinjection;
when a certain cell in the plurality of adherent cells is visited by a certain micropipette manipulated by a corresponding micromanipulator, control the corresponding micromanipulator to cause said certain micropipette to pierce into said certain cell, and control the gas pressure provider to cause said certain micropipette to inject a predetermined amount of the sample into said certain cell;
obtain XY locations of micropipette tips of the plurality of micropipettes;
control the camera to capture the cell image;
determine, from the cell image, XY locations of the respective cells; and
determine the injection sequence according to the XY locations of micropipette tips of the plurality of micropipettes and the XY locations of the respective cells;
wherein the injection sequence is determined by a process comprising:
constructing an undirected graph G=(V, E) wherein:
V={node(l)|l=0, 1, . . . , nq} is a set of nq+1 nodes, n being a number of cells in the plurality of adherent cells, q being a number of micropipettes in the plurality of micropipettes, V being partitioned into n clusters of nodes, the n clusters of nodes being denoted as V0, V1, . . . , Vn, the q micropipettes being denoted as P1, P2, . . . , Pq;
E={eij|i, j=0, 1, . . . , nq} is an edge set representing edges joining node(i) and node(j) with a cost cij in the graph G;
V0 is given by V0={node(0)} where node(0) represents P1;
Vm, m∈{1, 2, . . . , n}, is given by Vm={node((m−1)q+k)|k=1, 2, . . . , q}, where node((m−1)q+1), node((m−1)q+2), . . . , node(mq) respectively represent Cm, C′m(2), C′m(3), . . . , C′m(q) in which Cm is an mth real cell in the plurality of adherent cells, and
C′m(k), k∈{2, . . . , q}, is a kth virtual cell of the mth real cell;
Pk, k∈{1, 2, . . . , q}, has a coordinate (uPk, vPk) determined from the XY locations of the micropipette tips;
Cm, m∈{1, 2, . . . , m}, has a coordinate (um, vm) determined from the XY locations of the respective cells;
C′m(k), k∈{2, . . . , q}, has a coordinate (u′m(k), v′m(k)) given by (u′m(k), v′m(k))=(um+uP1−uPk, vm+vP1−vPk); and
cij, i, j∈{1, 2, . . . , nq}, is given by a Euclidean distance between node(i) and node(j);
numerically solving an equality-generalized traveling salesman problem (E-GTSP) defined by G to identify an ordered sequence of nodes containing one node from each of V0, V1, . . . , Vn such that the ordered sequence of nodes forms a minimum cost cycle; and
obtaining the injection sequence from the ordered sequence of nodes.
|