| CPC G06T 5/50 (2013.01) [G06N 3/043 (2023.01); G06N 3/045 (2023.01); G06N 3/088 (2013.01); G06T 3/60 (2013.01); G06T 2207/20084 (2013.01); G06T 2207/30041 (2013.01)] | 4 Claims |
|
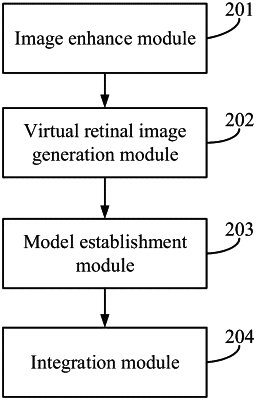
1. A method, comprising:
1) optimizing an objective function with a chaotic supply-demand algorithm to enhance a real retinal image to obtain an enhanced real retinal image;
2) synthesizing a virtual retinal image by a hybrid image generation method;
3) stablishing a parallel multi-layer decomposed interval type-2 intuitionistic fuzzy convolutional neural network model based on the virtual retinal image and the enhanced real retinal image; and
4) integrating outputs from a plurality of parallel multi-layer decomposed interval type-2 intuitionistic fuzzy convolutional neural network models as a final classification result;
wherein
1) is implemented as follows:
1.1) performing function transformation M on the real retinal image to obtain an enhanced output image:
EI(i,j)=M(I(i,j)|θ) (1)
where I(i, j) denotes a part of the real retinal image, and EI(i, j) denotes a corresponding part of the enhanced retinal image, i, j=1, 2, . . . , n; θ=(r, β, ρ, σ) is an undetermined parameter of the function (1);
M(I(i, j)|θ)=M(I(i, j)|r, β, ρ, σ)=rP/(s(i, j)+β)(I(i, j)−ρ×P(i, j))+P(i, j)σ denotes an image enhancement function, P(i, j)=Σp=1nΣq=1nP(p, q)/n2 denotes the average of local pixels of the real retinal image, s(i, j)=(Σp=1nΣq=1n(P(p, q)−P(i, j))2)1/2/n denotes a mean square error of local pixels of the real retinal image, P(p, q) denotes a pixel, n denotes a number of local pixels of the real retinal image, and P denotes a mean of all pixels;
1.2) setting a respective objective function J(θ) according to requirements of image enhancement, and obtaining parameter values when the objective function is optimized by the chaotic supply-demand algorithm, thus obtaining a reasonable image enhancement transformation function, and obtaining the enhanced real retinal image:
J(θ)=npe(EI(θ))×log(log(EI(θ)))×entropy(EI(θ)) (2)
where J(θ) denotes the objective function, npe(EI(θ)) denotes the number of pixels at an edge of the enhanced output image, log(log(EI(θ))) denotes the Sobel operator for a density at the edge of the enhanced output image, entropy(EI(θ))=−Σt=1256pt log2pt, where pt denotes a probability of the tth brightness level of the enhanced image;
the chaotic supply-demand algorithm comprises:
1.2.1) initializing market populations:
given the number of populations is Np and the dimensionality of a product price vector pi and of a production quantity vector qi is dim(θ)=4, determining a value range for pi and qi according to a search range for parameters in each dimension in a parameter vector θ=(r, β, ρ, σ), pij=[pj,pj], qij=[qj,qj];
selecting, for pij and qij, uniformly distributed random numbers in a unit interval respectively to obtain an initial unit product price population pi(0) and quantity population qi(0);
iteratively calculating a two-dimensional Ikeda map by respectively using pij(0) and qij(0) as initial values, to obtain a candidate initial product price population pi and quantity population qi by chaos iteration, 1≤i≤NpNT, where NT denotes a number of iterations;
for pij and qij in each dimension, performing linear transformation to obtain a candidate initial product price pi and quantity qi; and
calculating, according to Formula (2), an objective function value J(pi) and J(qi) respectively for the price and quantity of each product in a population and then normalizing, respectively comparing the objective function values J(pi) and J(qi) with the uniformly distributed random numbers, and selecting Np product prices and quantities to form an initial production price population and an initial quantity population;
1.2.2) determining the value of parameters and calculating an initial optimal product:
comparing the objective function values of the price and quantity of a product in the initial production price population and in the initial quantity population, respectively, and replacing pi with qi if J(pi)<J(qi), where the product price with the greatest objective function value is pbest=argmax1≤i≤NpJ(pi);
1.2.3) performing the following iteration process when the number of iterations t≤Ter, where Ter denotes a maximum number of iterations:
calculating an absolute variance of the objective function for the quantity of a product in a population, normalizing, and selecting the product quantity qk as an equilibrium quantity point qe according to an roulette method; while for the determination of an equilibrium point for the price of a product, comprising two stages: in the first stage, at t≤Ter/2, calculating the absolute variance of the objective function for the price of a product in a population, normalizing, and selecting the product price pl as an equilibrium point pe according to the roulette method, and in the second stage, at t>Ter/2, using the average of the product price in the population as the equilibrium point for the price of a product;
comparing the objective function values, replacing pi(t+1) with qi(t+1) if J(pi(t+1))<J(qi)(t+1)), pb(t+1)=argmax1≤m≤NpJ(pm(t+1)), if J(pb(t+1))>J(pbest), then pbest=pb(t+1), otherwise keeping pbest unchanged; and disturbing by logistic chaotic mapping if pbest remains unchanged after ten successive iterations and Ter has not yet been reached;
1.2.4) at the end of iteration, outputting an optimal solution pbest, where an enhanced image EI=M(I|pbest) is the enhanced real retinal image.
|