| CPC G06Q 10/06315 (2013.01) [G06Q 10/04 (2013.01); G06Q 10/06313 (2013.01); G06V 10/752 (2022.01)] | 20 Claims |
|
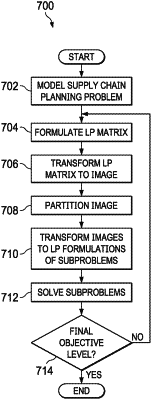
1. A system of solving a supply chain planning problem modeled as a linear programming problem, comprising:
a computer, comprising a processor and memory, the computer further comprising an image rendering engine, an image processing engine, a decomposition module, and a solver;
the image rendering engine configured to:
generate pixels of a supply chain problem image, the pixels representing links between constraints and variables of the linear programming problem;
the image processing engine configured to:
identify one or more contours of the supply chain problem image using a machine-learning model trained using a convolutional neural network and contour-labeled images received from the image rendering engine;
the decomposition module configured to:
determine a partition comprising at least two components linked by a first contour is more balanced than a partition comprising the at least two components linked by a second contour; and
the solver configured to:
formulate at least two decomposed subproblems sharing one or more complicating constraints associated with at least one of the one or more contours; and
solve the at least two decomposed subproblems to generate a solution to the supply chain planning problem.
|