| CPC G06Q 10/06315 (2013.01) [G06K 7/10722 (2013.01); G06K 7/1413 (2013.01); G06Q 10/083 (2013.01); G06Q 10/087 (2013.01); G06Q 50/04 (2013.01)] | 20 Claims |
|
1. A system of efficiently solving subsequent runs of a supply chain planning problem to reduce computer solve time, wherein the supply chain planning problem is modeled as a multi-objective hierarchical linear programming problem, comprising:
the computer, comprising a processor and memory, the computer solves the supply chain planning problem by:
receiving supply chain input data for the supply chain planning problem;
modeling the supply chain planning problem as a multi-objective hierarchal linear programming problem having a first objective and at least one additional objective, wherein the first objective and the at least one additional objective are ordered and defined by an objective hierarchy, and based, at least in part, on the supply chain input data;
solving a base run of the multi-objective hierarchical linear programming problem for the first objective and the at least one additional objective;
generating a base plan by converting a solution of the base run of the multi-objective hierarchical linear programming problem;
receiving one or more changes to the supply chain input data;
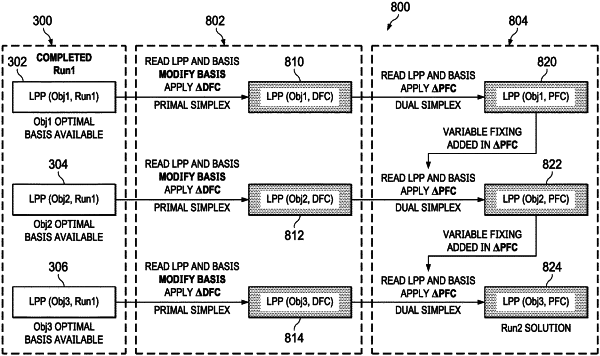
identifying primal feasibility changes of the one or more changes that affect only primal feasibility;
identifying dual feasibility changes of the one or more changes that affect only dual feasibility;
loading the multi-objective hierarchical linear programming problem and a first optimal basis of the first objective of the base run;
applying the dual feasibility changes;
modifying the first optimal basis of the first objective of the base run to generate a first starting basis for a new run;
solving the multi-objective hierarchical linear programming problem for the first objective of the new run using the first starting basis and a primal simplex method;
modifying a second optimal basis of the first objective of the new run to generate a second starting basis;
applying the primal feasibility changes;
solving the multi-objective hierarchical linear programming problem for the first objective using a dual simplex method and the second starting basis;
iteratively solving, according to the order specified by the objective hierarchy, each of the at least one additional objective of the multi-objective hierarchical linear programming problem for the new run, wherein decision variables for each subsequent objective are fixed at upper and lower bounds corresponding to objectives higher in the objective hierarchy that have already been solved; and
generating a new supply chain plan based, at least in part, on a solution of the new run.
|