| CPC G06Q 10/06311 (2013.01) [G06F 9/5038 (2013.01); G06N 3/006 (2013.01); G06F 9/4887 (2013.01)] | 1 Claim |
|
1. A method for scheduling resource-constrained project by Invasive Weed Optimization (IWO), comprising the following processes:
1) supposing a project being comprised of a set of activities J={0, 1, 2, . . . , n+1}, wherein the activities 0 and n+1 in this set are dummy activities, and represent the beginning and end of the project only without relating to the time and resources; j denotes a certain activity in the set, apart from the dummy activities, j∈J, Pj denotes a set of immediate predecessor activities of j, and Sj denotes a set of immediate successor activities of j; tj denotes the time duration of activity j, stj denotes the start time of the activity j; the project requires k kinds of resources, q denotes one of these resources, rjq denotes the demand amount for the resource q in unit time in the activity j, bq is maximum supply of the resource q in unit time; the time duration of project can be discretized, e.g. d={1, 2, . . . , T} where d is the timing of the discretized time duration, and T is the total time period of project; Ad={j|stj<d≤stj+tj} where Ad is the set of activities that are being executed at the timing d;
building up the mathematical model for optimizing the resource-constrained project scheduling can be established below on the basis of the above assumption;
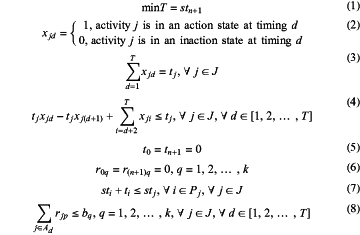 Where
Equation (1) is the objective function, i.e. the minimized time period of project;
Equation (2) is the decision variable;
Equation (3) expresses that each activity must be completed within a specified duration;
Equation (4) expresses that, once activity j started, it cannot be interrupted before completion;
Equations (5) and (6) express that the duration and resource demand are zero in the dummy activities 0 and n+1;
Equation (7) expresses the immediate predecessor/successor constraints, activity j can be initiated after all of these immediate predecessor activities were completed;
Equation (8) expresses a resource constraint, and the demand for a certain resource in all activities being running at the timing d is no more than the maximum supply of the resource in unit time;
2) optimizing the solution by IWO in the following steps:
Step 1: Setting parameters:
Setting initial population size Qsize, maximum population number Qmax, maximum seed number Smax, minimum seed number Smin, initial standard deviation σinit, final standard deviation σfinal, maximum iteration number itermax and non-linear harmonic index N;
Step 2: Initializing population:
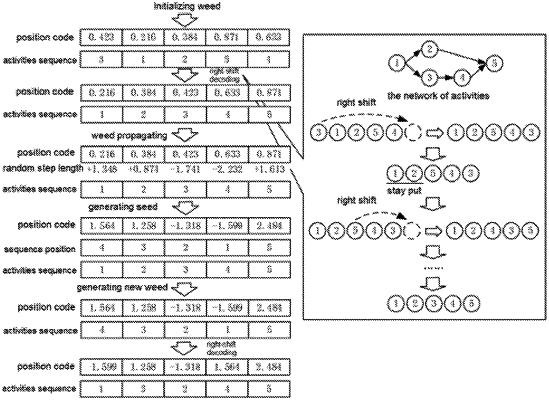
Initializing the weed population, wherein each individual weed includes a first code layer and a second code layer; the first code includes n+1 decimals between 0 and 1 that are generated randomly, to form a position code denoting the position of the weed; the second code layer includes a plurality of numbers denoting the sequence of activities, where each number corresponds to the sequence position of each decimal, as all the decimals are sequenced from small to large, such that all of these numbers become an activity sequence; the process of converting the position code in the first code layer to the activity sequence in the second code layer is called a conversion; each activity sequence, which corresponds to an individual weed, is a feasible solution for project scheduling, and its corresponding position code in the first code layer denotes the position of the feasible solution; meanwhile, as there are the immediate predecessor/successor constraints between the project activities, it is necessary to adjust the generated activity sequence through the right-shift decoding strategy, to make it become the eligibly feasible solution in compliance with the immediate predecessor/successor constraints, using the following ways:
Starting from the first position on the activity sequence, determine whether there is an immediate predecessor activity in the sequence after the activity; if not, it means that the immediate predecessor/successor activities have ended, thereby this activity can be initiated, and the position denoted by the sequence number in the activity sequence is unchanged; if there is an immediate predecessor activity in the sequence after this activity, it means that the immediate predecessor activities of this activity have not yet ended, thereby this activity cannot be initiated, and its sequence number needs to move backward to the last position of the sequence; then continuing such determination for all activities in the sequence, until an complete activity sequence that meets the immediate predecessor or successor constraints is obtained, and such activity sequence is an eligible feasible solution for the project; the initial weed population is formed by Qsize weed individuals that generated by the population initialization and meet the eligible feasible solution;
Step 3: Executing an iteration of the weed population, and calculating the fitness value of the weed;
Multiplying the reciprocal of the objective function (1/T) by the coefficient C as the fitness function Fitness, i.e. Fitness=C T, C is a constant, to calculate the fitness value of all weed individuals in the population;
Step 4. Calculating the number of seeds propagated by each individual weed in the population, and updating the standard deviation of this iteration;
the number of seeds, weed, produced in the reproduction process of each individual weed is proportional to the fitness value f of the weed, the equation is as follows:
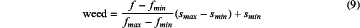 Where fmax is the maximum value of the fitness value of weeds in the population, and fmin is the minimum value of the fitness value of weeds in the population;
The seeds produced by weed propagation are spread around the weeds by a normal distribution with a mean value of 0 and a standard deviation of σ; The distance between the seed and the weed is called a random step D=[−σ, σ], a varies continuously as the iteration progresses, and its equation is as follows:
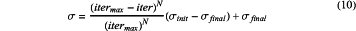 Where, iter is the current number of executed iterations of the weed population;
Step 5: Generating seeds through weeds propagation, subsequently new weed populations are formed by merging weeds from the generated seeds with the original weed population:
firstly the number of seeds, weed, and the related the standard deviation normal distribution σ, that are generated by the weed propagation, are calculated by equations (9) and (10); a new position obtained in the solution is called the seed, whose position code is the seed position code, that is, the seed position code can be obtained according to the weed position code and the random step length D; then performing the same operation in the step 2, converting the seed position codes to the activity sequence, performing a right-shift decoding to make the activity sequence become the eligibly feasible solution, thereby the seed grows into a weed; in the meantime, the seed position code becomes a weed position code, this code, together with the sequence of activities after the right-shift decoding, constitute the first and second code layers for a new individual weed; lastly merging all weeds from the seeds with the original weed population to obtain a new weed population;
Step 6. Adjusting whether the size of the weed population is greater than Qmax; if so, go to step 7; otherwise, go to step 3;
Step 7. Calculating the fitness value of the weeds in the population and selecting Qsize individuals pursuant to the principle of “struggle for existence”;
With the propagation of weeds, when the size of weed population exceeds the capacity of the environment, it is necessary to determine the maximum size of weed population in order to restrict the propagation of weeds, and retain elite weed individuals while eliminate the others through the criteria of survival of the fittest, then select Qsize weed individuals having high fitness value to form a new population;
Step 8. Determining whether the number of iterations equal to itermax; if so, output the optimal solution and end the calculation; otherwise, go to step 3 to execute a new iteration process.
|