| CPC G01R 33/4625 (2013.01) [G04F 5/14 (2013.01); H03L 7/26 (2013.01)] | 7 Claims |
|
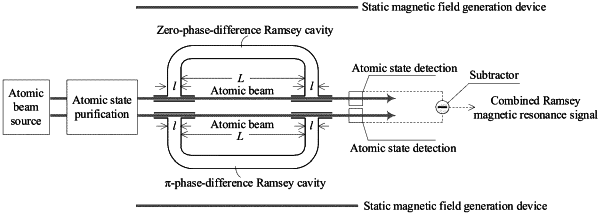
1. An atomic beam magnetic resonance method based on combined separated oscillatory fields (SOFs), comprising:
step 1, generating, by an atomic beam source, two identical atomic beams;
step 2, performing atomic state purification treatment on the two identical atomic beams to generate two identical state-purified atomic beams;
step 3, exciting, by zero-phase-difference SOFs, one of the two identical state-purified atomic beams to perform atomic beam magnetic resonance to thereby obtain a first atomic beam magnetic resonance signal; and exciting, by π-phase-difference SOFs, the other of the two identical state-purified atomic beams to perform atomic beam magnetic resonance to thereby obtain a second atomic beam magnetic resonance signal, wherein the zero-phase-difference SOFs and the π-phase-difference SOFs have the same interaction length, the same drift length, and the same oscillatory field strength; and
step 4, performing subtraction operation on the first atomic beam magnetic resonance signal and the second atomic beam magnetic resonance signal to thereby generate a combined Ramsey magnetic resonance signal, wherein a Ramsey transition probability function describing the combined Ramsey magnetic resonance signal is expressed as:
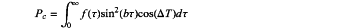 where τ represents a duration of interaction between an atom and an oscillatory field; l represents the interaction length; ƒ(τ) represents an interaction duration distribution function; b represents a strength of the oscillatory field; Δ=ω−ω0, ω represents an angular frequency of the oscillatory field, and ω0 represents an atomic transition angular frequency; and T represents a free drift duration of the atom in an oscillatory field-free region of a length L.
|